Ceci est une prévisualisation d'un thème de Hitskin.com
Installer le thème • Retourner sur la fiche du thème
Bref aperçu sur l'infini.
+6
Plaristes Evariste
Darbut
Frère Barnabé
Minos de Rhadamanthe
Edouard de Montmonrency
Esculape
10 participants
Page 5 sur 6
Page 5 sur 6 •  1, 2, 3, 4, 5, 6
1, 2, 3, 4, 5, 6 
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Esculape a écrit:Conclusion : Ne plus réfléchir aujourd'hui à partir de la Théorie du Big bang d'hier toujours correcte dans ses grandes lignes mais considérablement enrichie. Et c'est cet enrichissement primordial qu'il est impératif de connaître.
Amicalement
J'ai toujours l'impression, c'est juste une impression que la physique quantique à remise en question les fondamentaux de la physique et que la théorie du Big Bang en fait partie. Je me trompe?

Oligark- Impétrant

- Messages : 526
Date d'inscription : 31/01/2022
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Oligark a écrit:Esculape a écrit:Conclusion : Ne plus réfléchir aujourd'hui à partir de la Théorie du Big bang d'hier toujours correcte dans ses grandes lignes mais considérablement enrichie. Et c'est cet enrichissement primordial qu'il est impératif de connaître.
Amicalement
J'ai toujours l'impression, c'est juste une impression que la physique quantique à remise en question les fondamentaux de la physique et que la théorie du Big Bang en fait partie. Je me trompe?
"Je me trompe?"
Hélas, oui, complètement !
La mécanique quantique n'a absolument pas remis en question la physique classique* !
La physique classique étudie les phénomènes à notre échelle et la mécanique quantique étudie les lois régissant les interactions entre les particules qui constituent les atomes dont est formée la matière.
Quant à la théorie du Big bang, qui relève de la théorie de la Relativité générale, elle appartient à la cosmologie qui est l'étude de l'Univers en sa globalité et n'a rien à voir avec la mécanique quantique, sauf à l'hypothétique "instant zéro" non encore compris car on a besoin d'une nouvelle théorie unifiant la Relativité générale et la mécanique quantique, nouvelle théorie non encore découverte. (Peut-être la théorie des cordes ou bien la théorie de la gravitation quantique à boucles apporteront elles une solution, mais ce n'et pas encore sûr.)
La mécanique quantique et la Relativité générale sont des théories contre-intuitives où "l'impression" perd toute signification.
Amicalement.
*Un exemple, parmi tant d'autres : Lorsque les Américains ont réussi leurs six débarquement sur la lune, ils ont utilisé pour leur calculs de trajectoire UNIQUEMENT la mécanique newtonienne et n'ont pas eu besoin de faire appel à la théorie de la Relativité.
Même remarque pour la mise en orbite autour du point de Lagrange L2 du télescope James Webb.
Les cinq points de Lagrange eux mêmes ont été calculés à l'aide des équations de la mécanique céleste, elle même de stricte obédience à la mécanique newtonienne.
Enfin, toute la physique classique est basée sur la mécanique de Newton et les équations de Maxwell (pour ne citer que les principales).

Esculape- Chef

- Messages : 1885
Date d'inscription : 31/07/2021
Age : 97
Localisation : Ile de France
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Merci je me sens déjà moins bête.
C'est également à ces théories que je pensais. J'ai lu il y'a peu qu'il y'avait un lien entre multivers et boucle mais je n'ai pas encore tout capté. Oui je me souviens c'est fondé sur les probabilités des déplacements des particules. Dans le monde quantique tout est en rapport avec les probabilités.
Et on nous explique ceci :
Dans un univers unique où les événements se produisent un nombre limité de fois, les chercheurs peuvent calculer la probabilité relative qu'un événement se produise plutôt qu'un autre en comparant les nombres de fois que ces événements se produisent. Mais dans un multivers où tout se produit un nombre infini de fois, un tel décompte est impossible et, dès lors, rien n'a plus de chances de se produire que le reste. On peut faire les prédictions que l'on veut, elles sont amenées à se réaliser dans l'un ou l'autre univers, mais cela ne nous renseigne en rien sur ce qui va se passer dans notre propre univers.
C'est votre exemple avec les dés je me trompe? Il y'avait un parallèle avec la probabilité qu'un évènement arrive. Du coup je pense à Bayes
Esculape a écrit:Peut-être la théorie des cordes ou bien la théorie de la gravitation quantique à boucles apporteront elles une solution, mais ce n'et pas encore sûr.)
C'est également à ces théories que je pensais. J'ai lu il y'a peu qu'il y'avait un lien entre multivers et boucle mais je n'ai pas encore tout capté. Oui je me souviens c'est fondé sur les probabilités des déplacements des particules. Dans le monde quantique tout est en rapport avec les probabilités.
Et on nous explique ceci :
Dans un univers unique où les événements se produisent un nombre limité de fois, les chercheurs peuvent calculer la probabilité relative qu'un événement se produise plutôt qu'un autre en comparant les nombres de fois que ces événements se produisent. Mais dans un multivers où tout se produit un nombre infini de fois, un tel décompte est impossible et, dès lors, rien n'a plus de chances de se produire que le reste. On peut faire les prédictions que l'on veut, elles sont amenées à se réaliser dans l'un ou l'autre univers, mais cela ne nous renseigne en rien sur ce qui va se passer dans notre propre univers.
C'est votre exemple avec les dés je me trompe? Il y'avait un parallèle avec la probabilité qu'un évènement arrive. Du coup je pense à Bayes

Oligark- Impétrant

- Messages : 526
Date d'inscription : 31/01/2022
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Oligark a écrit:Merci je me sens déjà moins bête.Esculape a écrit:Peut-être la théorie des cordes ou bien la théorie de la gravitation quantique à boucles apporteront elles une solution, mais ce n'et pas encore sûr.)
C'est également à ces théories que je pensais. J'ai lu il y'a peu qu'il y'avait un lien entre multivers et boucle mais je n'ai pas encore tout capté. Oui je me souviens c'est fondé sur les probabilités des déplacements des particules. Dans le monde quantique tout est en rapport avec les probabilités.
Et on nous explique ceci :
Dans un univers unique où les événements se produisent un nombre limité de fois, les chercheurs peuvent calculer la probabilité relative qu'un événement se produise plutôt qu'un autre en comparant les nombres de fois que ces événements se produisent. Mais dans un multivers où tout se produit un nombre infini de fois, un tel décompte est impossible et, dès lors, rien n'a plus de chances de se produire que le reste. On peut faire les prédictions que l'on veut, elles sont amenées à se réaliser dans l'un ou l'autre univers, mais cela ne nous renseigne en rien sur ce qui va se passer dans notre propre univers.
C'est votre exemple avec les dés je me trompe? Il y'avait un parallèle avec la probabilité qu'un évènement arrive. Du coup je pense à Bayes
Bonjour Oligark,
Attention à ceci :
La fonction d'onde, solution de l'équation de Schrödinger, évolue de façon parfaitement déterministe.
C'est au moment où on effectue une mesure que cette fonction d'onde, qui contient tous les états différents et simultanés d'un système quantique, s'effondre en se fixant sur un seul état. Les physiciens anglophones l'appellent la "réduction du vecteur d'état".
Dans le cas de l'HPOTHETIQUR multivers contenant un nombre infini d'Univers, il est inévitable qu'au moins deux Univers soient rigoureusement jumeaux.
Il est possible aussi que, chaque Univers y ayant connu son propre Big bang, démarre avec des conditions initiales différentes.
La théorie nous montre alors que la vie, telle que nous la connaissons, est apparue dans un Univers dont les conditions sont conformes à celles exigées pour que la vie puiss y exister.
Il s'agit alors du multivers de niveau I. Les théoriciens, se fondant sur des développements de très hautes mathématiques, en sont arrivés à la conclusion qu'il pourrait exister un multivers de niveau II constitué de multivers de niveau I !
Il existerait peut-être aussi un multivers de niveau III appelé "multivers quantique"
Finalement, la théorie va jusqu'à suggérer que l'Univers global serait une structure mathématique.
N'oublions pas que déjà Galilée affirmait : "La Nature parle le langage mathématique" et, de nos jours, les mathématiciens et les physiciens sont d'accord pour dire que l'on découvre les mathématiques tout comme on découvre les lois de la physique.
On dit que l'Univers est mathématique et on va même plus loi en affirmant "La mathématique EST l'Univers !"
La conséquence fâcheuse est qu'il est impossible de vulgariser sans la déformer la physique d'aujourd'hui car elle est écrite dans le langage mathématique, celui de l'Univers et il est impossible de traduire fidèlement le langage mathématique dans nos langues habituelles.
Déjà, Cervantès, le père de don Quichotte, affirmait avec raison : "Lire une traduction c'est regarder l'envers d'un tapis."
Eh bien, c'est encore pire avec la langue mathématique car elle est intraduisible en français comme en n'importe quelle autre langue.
Cordialement.

Esculape- Chef

- Messages : 1885
Date d'inscription : 31/07/2021
Age : 97
Localisation : Ile de France
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Esculape a écrit:...On dit que l'Univers est mathématique et on va même plus loin en affirmant "La mathématique EST l'Univers !"
...
Les scientistes ça osent tout, c'est même a ça qu'on les reconnaît.

Edouard de Montmonrency- Vénérable

- Messages : 20670
Date d'inscription : 02/01/2022
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
On reconnaît surtout les Grandes G..... débiles qui portent des jugements sur des sujets dont ils ignorent tout, c'est à ça qu'on reconnaît ce qu'ils sont, et il serait préférable pour eux qu'ils se fissent oublier.blablabla-le-couplet a écrit:Esculape a écrit:...On dit que l'Univers est mathématique et on va même plus loin en affirmant "La mathématique EST l'Univers !"
...
Les scientistes ça osent tout, c'est même a ça qu'on les reconnaît.

Esculape- Chef

- Messages : 1885
Date d'inscription : 31/07/2021
Age : 97
Localisation : Ile de France
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
... Oui, les scientistes, c'est la peste. (une foi totalitaire en une religion comme une autre)

Edouard de Montmonrency- Vénérable

- Messages : 20670
Date d'inscription : 02/01/2022
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Mais oui, mais oui.blablabla-le-couplet a écrit:... Oui, les scientistes, c'est la peste. (une foi totalitaire en une religion comme une autre)
Calmez vous où on va encore vous remettre la camisole !

Esculape- Chef

- Messages : 1885
Date d'inscription : 31/07/2021
Age : 97
Localisation : Ile de France
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Esculape a écrit:Mais oui, mais oui.blablabla-le-couplet a écrit:... Oui, les scientistes, c'est la peste. (une foi totalitaire en une religion comme une autre)
Calmez vous où on va encore vous remettre la camisole !
lol ... te voilà psychiatre mathématicien de l'Univers maintenant ;-) ... heureusement que le ridicule ne tue pas.

Edouard de Montmonrency- Vénérable

- Messages : 20670
Date d'inscription : 02/01/2022
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
INFIRMIER ! VITE !blablabla-le-couplet a écrit:Esculape a écrit:Mais oui, mais oui.blablabla-le-couplet a écrit:... Oui, les scientistes, c'est la peste. (une foi totalitaire en une religion comme une autre)
Calmez vous où on va encore vous remettre la camisole !
lol ... te voilà psychiatre mathématicien de l'Univers maintenant ;-) ... heureusement que le ridicule ne tue pas.
Napoléon est à nouveau en crise ! Donnez lui u sédatif et conduisez le à la chambre capitonnée.

Esculape- Chef

- Messages : 1885
Date d'inscription : 31/07/2021
Age : 97
Localisation : Ile de France
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Esculape a écrit: il est inévitable qu'au moins deux Univers soient rigoureusement jumeaux.
On peut penser que : chaque décision prise par un être à un effet sur l'Univers dans sa globalité?
Un peu comme la vision plus extrême que les battements d'aile d'un papillon provoquerait une tempête à l'autre bout de la planète.
Si on pense que notre action cause plusieurs effets, il en va de même pour chaque particules. Ce qui laisserait penser que chaque vecteur choisit amène à de nouveaux vecteurs. Mais cette suite n'est pas lisible car elle pourrait être comme une partie d'échec donc les coups sont calculables (à partir d'un nombre importants de coups joués bien entendu) uniquement à l'aide d'une machine dont la mémoire est bien supérieure à la notre.
Esculape a écrit:démarre avec des conditions initiales différentes.
J'ai ma réponse, c'est bon
Esculape a écrit:Eh bien, c'est encore pire avec la langue mathématique car elle est intraduisible en français comme en n'importe quelle autre langue.
Cordialement.
Par contre, je vais être barbant (j'essaye de comprendre) , on utilise pourtant des nombres que l'on peut expliquer en français, tout comme des formules, des théorèmes, de la géométrie.
Vous dîtes ça parce que ce sont deux langages différents?
Les langages informatiques sont différents mais ils sont tout de même à rapprocher des mathématiques. C'est un peu un mélange de français et de mathématiques d'ailleurs. Quand je dis français, je veux dire de la langue maternelle pour l'idée, le concept mis en application à l'aide de raisonnements logiques.

Oligark- Impétrant

- Messages : 526
Date d'inscription : 31/01/2022
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Pour ce qui concerne l'évolution de deux Univers jumeaux, vous avez raison, ne serait-ce que comme conséquence de "l'effet papillon"Oligark a écrit:Esculape a écrit: il est inévitable qu'au moins deux Univers soient rigoureusement jumeaux.
On peut penser que : chaque décision prise par un être à un effet sur l'Univers dans sa globalité?
Un peu comme la vision plus extrême que les battements d'aile d'un papillon provoquerait une tempête à l'autre bout de la planète.
Si on pense que notre action cause plusieurs effets, il en va de même pour chaque particules. Ce qui laisserait penser que chaque vecteur choisit amène à de nouveaux vecteurs. Mais cette suite n'est pas lisible car elle pourrait être comme une partie d'échec donc les coups sont calculables (à partir d'un nombre importants de coups joués bien entendu) uniquement à l'aide d'une machine dont la mémoire est bien supérieure à la notre.Esculape a écrit:démarre avec des conditions initiales différentes.
J'ai ma réponse, c'est bonEsculape a écrit:Eh bien, c'est encore pire avec la langue mathématique car elle est intraduisible en français comme en n'importe quelle autre langue.
Cordialement.
Par contre, je vais être barbant (j'essaye de comprendre) , on utilise pourtant des nombres que l'on peut expliquer en français, tout comme des formules, des théorèmes, de la géométrie.
Vous dîtes ça parce que ce sont deux langages différents?
Les langages informatiques sont différents mais ils sont tout de même à rapprocher des mathématiques. C'est un peu un mélange de français et de mathématiques d'ailleurs. Quand je dis français, je veux dire de la langue maternelle pour l'idée, le concept mis en application à l'aide de raisonnements logiques.
Je dis en effet que la physique a atteint un tel degré de mathématisation que mathématique et physique finissent par se confondre.
La physique emploie, est contrainte d'employer, des concepts mathématiques terriblement abstraits ne correspondant à rien de concret pouvant être exposé en termes de langue naturelle quelle qu'elle soit.
Par exemple, la mécanique quantique fait appel au concept mathématique d'espace de Hilbert. C'est un espace pouvant atteindre un nombre infini de dimensions COMPLEXES, au sens de la théorie des nombres complexes. Intraduisible dans une langue naturelle.
En cosmologie, l'usage de la théorie de la Relativité générale impose les concepts de tenseurs, d'espaces de Riemann et hyperbolique dont la mathématique est trop sophistiquée, trop abstraite, pour pouvoir être traduite en langue naturelle.
Je suis le premier à le regretter car je voudrais tellement faire partager mon admiration et ma passion pour la physique moderne qui a porté très haut l'intelligence humaine.

Esculape- Chef

- Messages : 1885
Date d'inscription : 31/07/2021
Age : 97
Localisation : Ile de France
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Esculape a écrit:Par exemple, la mécanique quantique fait appel au concept mathématique d'espace de Hilbert. C'est un espace pouvant atteindre un nombre infini de dimensions COMPLEXES, au sens de la théorie des nombres complexes. Intraduisible dans une langue naturelle.
En cosmologie, l'usage de la théorie de la Relativité générale impose les concepts de tenseurs, d'espaces de Riemann et hyperbolique dont la mathématique est trop sophistiquée, trop abstraite, pour pouvoir être traduite en langue naturelle.
Je suis le premier à le regretter car je voudrais tellement faire partager mon admiration et ma passion pour la physique moderne qui a porté très haut l'intelligence humaine.
Mais le but à atteindre, ce que l'on cherche. Il doit d'abord être pensé en Français. Lorsque vous utilisez une équation, vous cherchez à démontrer quelque chose. Vous ne partez pas d'un concept mathématique sans avoir réfléchi sur son sens et son utilité. L'abstraction vient après la compréhension du concept.
Si on parle de Riemann
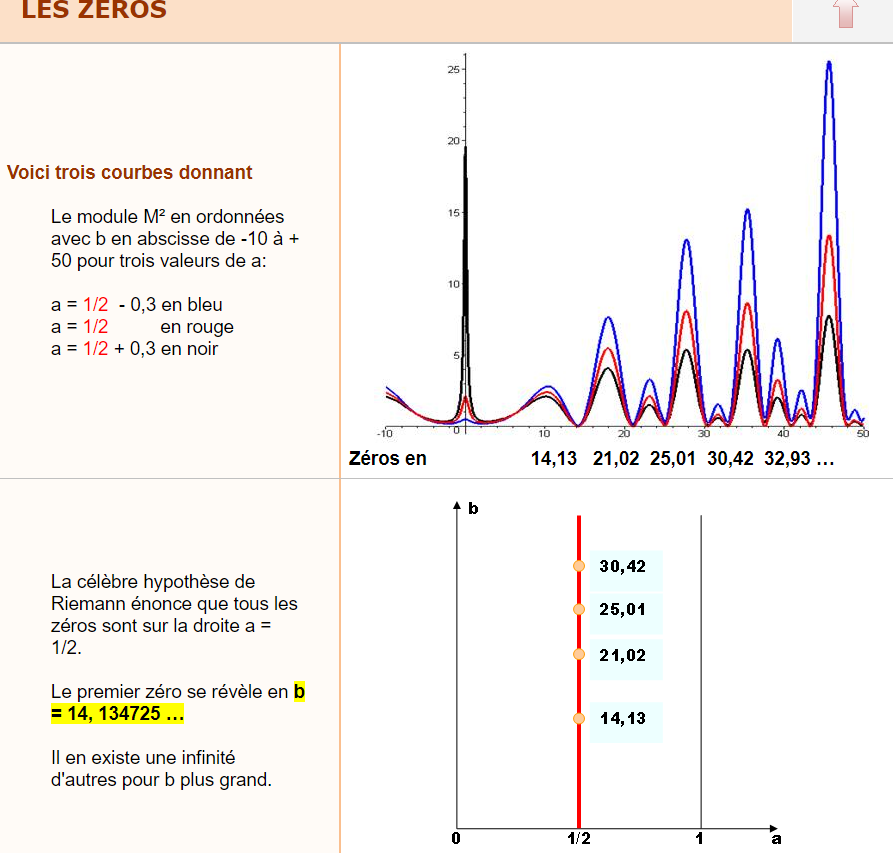
Mais alors je vous demande pourquoi chercher la répartition des nombres premiers?
Quel était son but?
futura-sciences a écrit: fit alors l'hypothèse que toutes ses solutions non triviales devraient suivre, dans le plan complexe, une ligne d'équation ½ + it et, de fait, présenter une composante réelle toujours égale à ½. Depuis, les mathématiciens ont trouvé des milliards de zéros non triviaux à la fonction zêta et tous présentent effectivement une composante réelle égale à ½. Cependant, l'universalité de la théorie reste toujours à prouver
------------------------------------------------------------------------------------------------------------------
L'effet tunnel désigne la propriété que possède un objet quantique de franchir une barrière de potentiel même si son énergie est inférieure à l'énergie minimale requise pour franchir cette barrière. C'est un effet purement quantique, qui ne peut pas s'expliquer par la mécanique classique.
Si l'objet quantique, c'est tout élément de la structure microscopique de la matière et du rayonnement : atomes, électrons, photons.
Je ne comprends pas. C'est parce que nous sommes sur une structure microscopique que l'énergie de l'objet quantique n'a pas besoin de la même énergie?
C'est uniquement une question d'échelle?
-------------------------------------------------------------------------------------------------------------------
Note
[L'espace de Hilbert il faudrait comprendre les espaces vectoriels de dimension infinie ]
[Il faut savoir utiliser tout les types d'espaces vectoriels]
Théorème de Hahn-Banach : Outil d'analyse fonctionnelle

Oligark- Impétrant

- Messages : 526
Date d'inscription : 31/01/2022
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
.Oligark a écrit:Esculape a écrit:Par exemple, la mécanique quantique fait appel au concept mathématique d'espace de Hilbert. C'est un espace pouvant atteindre un nombre infini de dimensions COMPLEXES, au sens de la théorie des nombres complexes. Intraduisible dans une langue naturelle.
En cosmologie, l'usage de la théorie de la Relativité générale impose les concepts de tenseurs, d'espaces de Riemann et hyperbolique dont la mathématique est trop sophistiquée, trop abstraite, pour pouvoir être traduite en langue naturelle.
Je suis le premier à le regretter car je voudrais tellement faire partager mon admiration et ma passion pour la physique moderne qui a porté très haut l'intelligence humaine.
Mais le but à atteindre, ce que l'on cherche. Il doit d'abord être pensé en Français. Lorsque vous utilisez une équation, vous cherchez à démontrer quelque chose. Vous ne partez pas d'un concept mathématique sans avoir réfléchi sur son sens et son utilité. L'abstraction vient après la compréhension du concept.
Si on parle de Riemann
Mais alors je vous demande pourquoi chercher la répartition des nombres premiers?
Quel était son but?futura-sciences a écrit: fit alors l'hypothèse que toutes ses solutions non triviales devraient suivre, dans le plan complexe, une ligne d'équation ½ + it et, de fait, présenter une composante réelle toujours égale à ½. Depuis, les mathématiciens ont trouvé des milliards de zéros non triviaux à la fonction zêta et tous présentent effectivement une composante réelle égale à ½. Cependant, l'universalité de la théorie reste toujours à prouver
------------------------------------------------------------------------------------------------------------------
L'effet tunnel désigne la propriété que possède un objet quantique de franchir une barrière de potentiel même si son énergie est inférieure à l'énergie minimale requise pour franchir cette barrière. C'est un effet purement quantique, qui ne peut pas s'expliquer par la mécanique classique.
Si l'objet quantique, c'est tout élément de la structure microscopique de la matière et du rayonnement : atomes, électrons, photons.
Je ne comprends pas. C'est parce que nous sommes sur une structure microscopique que l'énergie de l'objet quantique n'a pas besoin de la même énergie?
C'est uniquement une question d'échelle?
-------------------------------------------------------------------------------------------------------------------
Note
[L'espace de Hilbert il faudrait comprendre les espaces vectoriels de dimension infinie ]
[Il faut savoir utiliser tout les types d'espaces vectoriels]
Théorème de Hahn-Banach : Outil d'analyse fonctionnelle
.
- Tout d'abord, il faut bien distinguer deux formes de recherches en mathématiques :
- En mathématiques pures,
- En mathématiques relatives à la physique.
On ne sait pas à l'avance si une découverte en mathématiques pures recevra ou non une application en physique. Par exemple, lorsque Hilbert a découvert les espaces qui portent son nom, il cherchait une méthode pour résoudre les équations intégro-différentielles sans se douter que ces espaces joueraient un rôle crucial en mécanique quantique. Même remarque pour l'analyse tensorielle en Relativité générale etc.
Pour ce qui concerne la fonction de Riemann et sa conjecture :
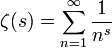
il faut savoir que s désigne une variable complexe. Cette conjecture qui énonce que les zéros de cette fonction appartiennent à la droite d'équation x = 1/2 relève de la mathématique pure et bien malin serait qui affirmerait que cette fonction n'aura jamais d'applications en physique !
Pour ce qui concerne la mathématique vue comme langage de la physique, commençons donc à réfléchir à cette profonde remarque de Paul Langevin :
"Les équations de la physique connaissent mieux la physique que les physiciens eux mêmes.".
Exemple :
Lorsque James Clerc Maxwell a découvert les quatre équations unifiant le champ électrique et le champ magnétique (ces équations étaient liées, imposées par le domaine de recherche !), il ne se doutait pas que seraient trouvées comme solutions à ses équations l'existence des onde électromagnétiques ni l'invariance de la vitesse de la lumière, point de départ de la Relativité restreinte !
Autre exemple :
Lorsqu'en 1915 Einstein publia son équation fondamentale de la Relativité générale, personne, pas même Einstein lui même, ne pouvait se douter que cette équation révélerait l'existence de :
- L'expansion de l'Univers,
- L'explication de l'avance du périhélie de mercure,
- Une déviation d'un rayon lumineux par son passage à proximité d'un corps massif,
- Des trous noirs,
- De l'effet Lens-Thirring,
- Des ondes gravitationnelles.
et j'en oublie probablement.
Voici je crois qui répond l'essentiel à vos questions qu'un contexte un peu difficile justifie qu'on de les pose.
Addendum.
En me relisant, je remarque que l'ai oublié de répondre à votre question concernant l'effet tunnel.
Une réponse complète exigerait un long développement.
Aussi, peut-être provisoirement, me bornerai-je à ceci :
La fonction d'onde d'une particule doit être interprétée comme la probabilité de présence d'une particule à l'instant t et au lieu x.
Si un obstacle (une barrière de potentiel) s'oppose au passage de la particule et si sa fonction d'onde n'est pas nulle au delà de cet obstacle, alors il existe une probabilité non nulle pour trouver la particule au delà de cet obstacle. Tel est, en gros, l'effet tunnel.

Esculape- Chef

- Messages : 1885
Date d'inscription : 31/07/2021
Age : 97
Localisation : Ile de France
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Vous avez répondu et plus encore. Merci, je sais à quoi m'en tenir.
J'ai compris que celui qui découvre certaines équations ne connaît pas encore obligatoirement leur utilité, leur application.
Ce qui me permet de comprendre pourquoi il faut maîtriser par exemple le champs électrique ou magnétique pour en découvrir de nouvelles.
je reviendrais dans quelques jours pour vous poser des questions sur cette partie.
J'ai compris que celui qui découvre certaines équations ne connaît pas encore obligatoirement leur utilité, leur application.
Ce qui me permet de comprendre pourquoi il faut maîtriser par exemple le champs électrique ou magnétique pour en découvrir de nouvelles.
je reviendrais dans quelques jours pour vous poser des questions sur cette partie.
Esculape a écrit:Lorsque James Clerc Maxwell a découvert les quatre équations unifiant le champ électrique et le champ magnétique (ces équations étaient liées, imposées par le domaine de recherche !), il ne se doutait pas que seraient trouvées comme solutions à ses équations l'existence des onde électromagnétiques ni l'invariance de la vitesse de la lumière, point de départ de la Relativité restreinte !

Oligark- Impétrant

- Messages : 526
Date d'inscription : 31/01/2022
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Oligark a écrit:Vous avez répondu et plus encore. Merci, je sais à quoi m'en tenir.
J'ai compris que celui qui découvre certaines équations ne connaît pas encore obligatoirement leur utilité, leur application.
Ce qui me permet de comprendre pourquoi il faut maîtriser par exemple le champs électrique ou magnétique pour en découvrir de nouvelles.
je reviendrais dans quelques jours pour vous poser des questions sur cette partie.Esculape a écrit:Lorsque James Clerc Maxwell a découvert les quatre équations unifiant le champ électrique et le champ magnétique (ces équations étaient liées, imposées par le domaine de recherche !), il ne se doutait pas que seraient trouvées comme solutions à ses équations l'existence des onde électromagnétiques ni l'invariance de la vitesse de la lumière, point de départ de la Relativité restreinte !
Et c'est avec plaisir que je vous répondrai car c'est justement la mission que je me suis donnée au départ d'aider en physique ceux intéressés par cette science fascinante.
J'ajoute que le passage de mon message que vous citez et qui a attiré votre attention prouve que vous en soupçonnez l'importance. Cette importance est due à la mathématisation quasi-totale de la physique tant en mécanique céleste, qu'en astrophysique, qu'en cosmologie et en mécanique quantique.
Vous avez mis le doigt sur l'essentiel.
Cordialement.

Esculape- Chef

- Messages : 1885
Date d'inscription : 31/07/2021
Age : 97
Localisation : Ile de France
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
J'ai acheté un tableau blanc pour schématiser des réflexions. Je crois que des modèles sont obligatoires lorsque de plus en plus d'éléments interagissent avec nos pensées. Par contre je me demande en ce moment, si la physique peut m'être utile pour développer des algorithmes. Je vais réfléchir à tout ça. Et me renseigner sur l'interaction entre physique maths et psychologie.

Oligark- Impétrant

- Messages : 526
Date d'inscription : 31/01/2022
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Tout ce que je puis vous préciser est que c'est la logique qui est indispensable pour créer un algorithme applicable à un problème donné indépendamment de l'origine de ce problème.Oligark a écrit:J'ai acheté un tableau blanc pour schématiser des réflexions. Je crois que des modèles sont obligatoires lorsque de plus en plus d'éléments interagissent avec nos pensées. Par contre je me demande en ce moment, si la physique peut m'être utile pour développer des algorithmes. Je vais réfléchir à tout ça. Et me renseigner sur l'interaction entre physique maths et psychologie.
La thèse d'Alonzo Church, un des plus brillants logiciens, s'énonce ainsi :
"La théorie des machines de Turing, la théorie des fonctions récursives et la théorie des algorithmes sont équivalentes."
On y voit bien, entre autres, que seule la logique intervient dans la théorie des algorithmes ainsi que dans leur élaboration.
Enfin, je me déclare incompétent pour juger l'importance de la psychologie en physique et en mathématiques mais j'affirme avec force que : "Pas de mathématiques, alors pas de physique", ces deux disciplines étant de plus en plus imbriquées par le truchement des lois (mathématiques !) qui régissent le comportement de l'Univers.
Cela s'explique quand on sait que l'on DECOUVRE les mathématiques tout comme on découvre les lois de la physique, donc celles de l'Univers car l'Univers EST mathématique.

Esculape- Chef

- Messages : 1885
Date d'inscription : 31/07/2021
Age : 97
Localisation : Ile de France
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
L'Univers mais la pensée humaine en fait elle totalement partie?
Peux t-on dire la pensée humaine est mathématique?
Oui la récursivité je l'ai étudié un peu. Turing, je vois ça comme une branche, une spécialité dans le domaine des mathématiques. La cryptologie en fait partie.
Peux t-on dire la pensée humaine est mathématique?
Oui la récursivité je l'ai étudié un peu. Turing, je vois ça comme une branche, une spécialité dans le domaine des mathématiques. La cryptologie en fait partie.

Oligark- Impétrant

- Messages : 526
Date d'inscription : 31/01/2022
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Je me déclare incompétent pour répondre à vos deux premières questions.Oligark a écrit:L'Univers mais la pensée humaine en fait elle totalement partie?
Peux t-on dire la pensée humaine est mathématique?
Oui la récursivité je l'ai étudié un peu. Turing, je vois ça comme une branche, une spécialité dans le domaine des mathématiques. La cryptologie en fait partie.
Pour la suite :
La récursivité est une chose, la théorie des fonctions récursives en est une autre.
La "Machine de Turing" est de stricte obédience logique, elle est en quelque sorte le modèle logique d'un ordinateur et son rapport avec la mathématique est plutôt lointain.

Esculape- Chef

- Messages : 1885
Date d'inscription : 31/07/2021
Age : 97
Localisation : Ile de France
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Alors en cherchant sur wiki :

c'est très étrange car cela suppose que certains calculs ne sont pas possible avec un algorithme.
Récursivement énumérable : renvoie encore à une autre notion. Vous êtes très rusé, vous avez fait tout de suite le lien avec ce que je fais en ce moment.
On se rapproche parfois de l'arbre décisionnel. Je suis obligé d'étudier les critères de décidabilité. Mais je suis toujours entrain de douter sur la définition de récursif ici=>On dit qu'un problème (de décision) P est décidable si l'ensemble A des éléments qui répondent « oui » à la question posée est récursif.
J'ai besoin d'un exemple pour chaque problème posé comme celui de l'arrêt.
def paradox (f) :
étrange (f,f)
paradox (f) s'arrête uniquement si et seulement si f(f) ne s'arrête pas.
Cela s'applique au calcul, j'utilise plutôt la sémantique. Sauf si le calcul me permet de répondre au problème de sémantique.
C'est pour cette raison que j'utilise plutôt la récursivité.
wiki a écrit:Les fonctions partielles récursives correspondent aux fonctions calculées par une machine de Turing. Selon la thèse de Church, la classe des fonctions partielles récursives est exactement l'ensemble des fonctions numériques pouvant être décrites par un algorithme (ou tout mécanisme de calcul).

c'est très étrange car cela suppose que certains calculs ne sont pas possible avec un algorithme.
wiki a écrit:Ensemble récursif
De façon cohérente avec la définition précédente, un ensemble récursif est un ensemble d'entiers naturels ou de n-uplets d'entiers naturels dont la fonction caractéristique est récursive. Cela signifie que l'on peut décider mécaniquement de l'appartenance ou non à cet ensemble. On dira également ensemble décidable, le problème de décision
wiki a écrit:En théorie de la calculabilité, formuler un problème de décision c'est se poser une question de décidabilité. Il s'agit en fait de rechercher l'existence d'un algorithme résolvant le problème et, s'il existe, de l'expliciter. On dit qu'un problème (de décision) P est décidable si l'ensemble A des éléments qui répondent « oui » à la question posée est récursif. De même, P est dit partiellement décidable, semi-décidable ou prouvable si l'ensemble A est récursivement énumérable. Et dans le cas contraire, où le problème P n'est ni décidable, ni partiellement décidable, il est dit indécidable. Il y a des problèmes fondamentaux qui sont indécidables, c'est le cas du problème de l'arrêt.
Récursivement énumérable : renvoie encore à une autre notion. Vous êtes très rusé, vous avez fait tout de suite le lien avec ce que je fais en ce moment.
On se rapproche parfois de l'arbre décisionnel. Je suis obligé d'étudier les critères de décidabilité. Mais je suis toujours entrain de douter sur la définition de récursif ici=>On dit qu'un problème (de décision) P est décidable si l'ensemble A des éléments qui répondent « oui » à la question posée est récursif.
J'ai besoin d'un exemple pour chaque problème posé comme celui de l'arrêt.
def paradox (f) :
étrange (f,f)
paradox (f) s'arrête uniquement si et seulement si f(f) ne s'arrête pas.
Cela s'applique au calcul, j'utilise plutôt la sémantique. Sauf si le calcul me permet de répondre au problème de sémantique.
C'est pour cette raison que j'utilise plutôt la récursivité.

Oligark- Impétrant

- Messages : 526
Date d'inscription : 31/01/2022
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
.
.
Bien que nous soyons loin du sujet de départ, je dois préciser que la théorie des fonctions récursives a son équivalent en informatique théorique: La notion de calculabilité.
Cette notion a été bien précisée par le logicien Alonzo Church avec sa belle théorie du "Lambda-calculus". Voir une version simplifiée :
Lambda-calcul — Wikipédia (wikipedia.org)
On notera que le langage LISP (LISt Processing) a été développé par le logicien McCarthy à partie de ce lambda-calculus.
.
Bien que nous soyons loin du sujet de départ, je dois préciser que la théorie des fonctions récursives a son équivalent en informatique théorique: La notion de calculabilité.
Cette notion a été bien précisée par le logicien Alonzo Church avec sa belle théorie du "Lambda-calculus". Voir une version simplifiée :
Lambda-calcul — Wikipédia (wikipedia.org)
On notera que le langage LISP (LISt Processing) a été développé par le logicien McCarthy à partie de ce lambda-calculus.

Esculape- Chef

- Messages : 1885
Date d'inscription : 31/07/2021
Age : 97
Localisation : Ile de France
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Langage intéressant mais pour l'IA je le trouve trop austère et demande beaucoup trop de temps.
Je reste sur des langages plus souples et plus universels. On a plus l'impression d'un langage expérimental que pratique. (C.L.O.S permet de faire des classes comme des objets.)
Mais c'est justement parce qu'on trouve d'abord une abondance dans cette civilisation que l'on peut apporter notre pierre à cette civilisation. Trouver ne veut pas dire que l'on y trouve son compte, c'est uniquement quelque chose de quantifiable. L'intelligence artificielle ne doit pas se borner au quantifiable, au calcul. D'ailleurs l'artificiel c'est une manière de tromper l'esprit humain. On peut aller dans ce sens comme la majorité des I.A.
C'est en essayant de reproduire l'esprit humain que l'on s'écarte de l'artificiel. Si l'on rentre dans ce paradigme,
on peut dire que l'esprit humain est proche des mathématiques si et seulement si les mathématiques ne sont pas appliquées comme des abstractions mais comme des "méthodes à pensées".
Nous comprenons le fonctionnement des réseaux neuronaux, la partie biologique est comprise encore une fois par les mathématiques. En comprenant notre biologie, nous comprenons qu'il existe des passerelles entre toutes ces disciplines.
Je reste sur des langages plus souples et plus universels. On a plus l'impression d'un langage expérimental que pratique. (C.L.O.S permet de faire des classes comme des objets.)
Mais c'est justement parce qu'on trouve d'abord une abondance dans cette civilisation que l'on peut apporter notre pierre à cette civilisation. Trouver ne veut pas dire que l'on y trouve son compte, c'est uniquement quelque chose de quantifiable. L'intelligence artificielle ne doit pas se borner au quantifiable, au calcul. D'ailleurs l'artificiel c'est une manière de tromper l'esprit humain. On peut aller dans ce sens comme la majorité des I.A.
C'est en essayant de reproduire l'esprit humain que l'on s'écarte de l'artificiel. Si l'on rentre dans ce paradigme,
on peut dire que l'esprit humain est proche des mathématiques si et seulement si les mathématiques ne sont pas appliquées comme des abstractions mais comme des "méthodes à pensées".
Nous comprenons le fonctionnement des réseaux neuronaux, la partie biologique est comprise encore une fois par les mathématiques. En comprenant notre biologie, nous comprenons qu'il existe des passerelles entre toutes ces disciplines.

Oligark- Impétrant

- Messages : 526
Date d'inscription : 31/01/2022
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
J'ai cité le langage LISP à titre historique bien que, amélioré de nos jours, il ait été utilisé dès ls premières recherches en IA.Oligark a écrit:Langage intéressant mais pour l'IA je le trouve trop austère et demande beaucoup trop de temps.
Je reste sur des langages plus souples et plus universels. On a plus l'impression d'un langage expérimental que pratique. (C.L.O.S permet de faire des classes comme des objets.)
Mais c'est justement parce qu'on trouve d'abord une abondance dans cette civilisation que l'on peut apporter notre pierre à cette civilisation. Trouver ne veut pas dire que l'on y trouve son compte, c'est uniquement quelque chose de quantifiable. L'intelligence artificielle ne doit pas se borner au quantifiable, au calcul. D'ailleurs l'artificiel c'est une manière de tromper l'esprit humain. On peut aller dans ce sens comme la majorité des I.A.
C'est en essayant de reproduire l'esprit humain que l'on s'écarte de l'artificiel. Si l'on rentre dans ce paradigme,
on peut dire que l'esprit humain est proche des mathématiques si et seulement si les mathématiques ne sont pas appliquées comme des abstractions mais comme des "méthodes à pensées".
Nous comprenons le fonctionnement des réseaux neuronaux, la partie biologique est comprise encore une fois par les mathématiques. En comprenant notre biologie, nous comprenons qu'il existe des passerelles entre toutes ces disciplines.
C'était l'époque où ne doutait de rien ! Depuis, les chercheurs dans ce domaine ont mis un bémol à leurs prétentions.
C'est ainsi que, assagi pour un temps, le concept d'IA a cédé la place aux "systèmes experts" et aux programmes "d'aide à la décision", et ces prétendues IA ne sont rien d'autre car elles ne recèlent pas un iota d'intelligence.
Quant à la mathématique, on est bien obligé de l'utiliser, non comme une abstraction mais bel et bien comme le langage de l'Univers. Mais là, on aborde un sujet très complexe où logique mathématique, mathématique et physique (classique, relativiste, astrophysique, cosmologie, mécanique quantique) s'intègrent indissolublement liées et nécessitent pour leur compréhension des connaissances de très hauts niveaux incompatibles ave ce dont on peut débattre sur un forum mais seulement dans le cadre des grands symposium réunissant les ténors mondiaux de ces disciplines.
Je ne suis évidemment pas un de ces ténors mais j'en comprends leurs travaux d'où ma remarque.

Esculape- Chef

- Messages : 1885
Date d'inscription : 31/07/2021
Age : 97
Localisation : Ile de France
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Esculape a écrit:J'ai cité le langage LISP à titre historique bien que, amélioré de nos jours, il ait été utilisé dès ls premières recherches en IA.Oligark a écrit:Langage intéressant mais pour l'IA je le trouve trop austère et demande beaucoup trop de temps.
Je reste sur des langages plus souples et plus universels. On a plus l'impression d'un langage expérimental que pratique. (C.L.O.S permet de faire des classes comme des objets.)
Mais c'est justement parce qu'on trouve d'abord une abondance dans cette civilisation que l'on peut apporter notre pierre à cette civilisation. Trouver ne veut pas dire que l'on y trouve son compte, c'est uniquement quelque chose de quantifiable. L'intelligence artificielle ne doit pas se borner au quantifiable, au calcul. D'ailleurs l'artificiel c'est une manière de tromper l'esprit humain. On peut aller dans ce sens comme la majorité des I.A.
C'est en essayant de reproduire l'esprit humain que l'on s'écarte de l'artificiel. Si l'on rentre dans ce paradigme,
on peut dire que l'esprit humain est proche des mathématiques si et seulement si les mathématiques ne sont pas appliquées comme des abstractions mais comme des "méthodes à pensées".
Nous comprenons le fonctionnement des réseaux neuronaux, la partie biologique est comprise encore une fois par les mathématiques. En comprenant notre biologie, nous comprenons qu'il existe des passerelles entre toutes ces disciplines.
C'était l'époque où ne doutait de rien ! Depuis, les chercheurs dans ce domaine ont mis un bémol à leurs prétentions.
C'est ainsi que, assagi pour un temps, le concept d'IA a cédé la place aux "systèmes experts" et aux programmes "d'aide à la décision", et ces prétendues IA ne sont rien d'autre car elles ne recèlent pas un iota d'intelligence.
Quant à la mathématique, on est bien obligé de l'utiliser, non comme une abstraction mais bel et bien comme le langage de l'Univers. Mais là, on aborde un sujet très complexe où logique mathématique, mathématique et physique (classique, relativiste, astrophysique, cosmologie, mécanique quantique) s'intègrent indissolublement liées et nécessitent pour leur compréhension des connaissances de très hauts niveaux incompatibles ave ce dont on peut débattre sur un forum mais seulement dans le cadre des grands symposium réunissant les ténors mondiaux de ces disciplines.
Je ne suis évidemment pas un de ces ténors mais j'en comprends leurs travaux d'où ma remarque.
Oui, il vient juste après le Fortran. Il est en avance ce langage car d'autres concepteurs vont copier plus ou moins des parties pour d'autres langages.
Oui vous avez bien compris que c'était une mauvaise formulation de parler d'intelligence. J'aime bien votre référence au langage de l'Univers. Vous aimez philosopher avec les mathématiques. Parfois les choses complexes peuvent être expliquer plus simplement par Esculape. Néanmoins, je sais désormais qu'il n'est pas conseiller de vulgariser certaines théories au risque de perdre des éléments en route.
Admettons que je ne veuille pas taper tout de suite sur google le résultat de l'invariance de la vitesse de la lumière.
Cette invariance remet en question autre chose? Vous avez parlez des champs magnétique et électrique, existe t-il un lien?
https://intelligence-artificielle.developpez.com/actu/290209/Un-systeme-d-intelligence-artificielle-apprend-les-lois-fondamentales-de-la-mecanique-quantique-selon-un-rapport-de-recherche/ a écrit:
« Tous les concepts chimiques et les propriétés physiques des molécules sont déterminés par l'équation électronique de Schrödinger et dérivent de la fonction d'onde de l'état de base. Ainsi, un modèle Machine Learning de structure électronique qui prédit directement la fonction d'onde de l'état fondamental permettrait non seulement d'obtenir toutes les propriétés de l'état fondamental, mais pourrait ouvrir des voies vers de nouvelles méthodes approximatives de chimie quantique basées sur une interface entre la ML et la chimie quantique », lit-on dans l’article des chercheurs.
Qu'est ce que la chimie quantique?

Oligark- Impétrant

- Messages : 526
Date d'inscription : 31/01/2022
Page 5 sur 6 •  1, 2, 3, 4, 5, 6
1, 2, 3, 4, 5, 6 
Page 5 sur 6
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum Hitskin.com
Hitskin.com









