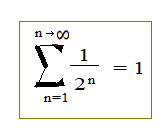Bref aperçu sur l'infini.
+6
Plaristes Evariste
Darbut
Frère Barnabé
Minos de Rhadamanthe
Edouard de Montmonrency
Esculape
10 participants
Page 4 sur 6
Page 4 sur 6 •  1, 2, 3, 4, 5, 6
1, 2, 3, 4, 5, 6 
 Dernière mise au point.
Dernière mise au point.
Il n'est rien de plus pénible, de plus déprimant, que d'être contré dans son métier par un quidam qui en ignore tout ! Il y a là un comportement inhabituel chez une personne supposée sensée a priori.
Formes indéterminées.
Bien entendu, d'après ce personnage, c'est moi, mathématicien de métier qui ne connaît rien aux mathématiques !
Récemment, j'ai évoqué ce que l'on appelle en mathématiques des formes indéterminées. Ce sont des expressions mathématiques pour lesquelles il est impossible d'affecter une valeur précise. Par exemple, l'expression indéterminée 0/0 n'a aucun sens. Il en est de même de n/0 quelque que soit le nombre n.
On rencontre aussi des formes indéterminées avec l'infini noté ∞.
Par exemple, les formes 1/∞, ∞/∞, ∞ multiplié par ∞, ∞/0, ∞ -∞ etc. sont des formes indéterminées ce qui signifie, retenez le bien ! qu'il est impossible de leur donner un résultat précis.
Or, cet intervenant qui, manifestement n'a que des connaissances rudimentaires en mathématiques a prétendu avec conviction, que ∞ - ∞ = ∞ ! Or, cette expression est fausse car on a vu qu'il est impossible de donner un résultat à une forme indéterminée, or ∞ - ∞ est une forme indéterminée d'où la contradiction de cet entêté ignorant qu'il ignore les mathématiques !
Eh bien, il a poussé l'inconscience jusqu'à vouloir donner une leçon de mathématiques à un mathématicien dument diplômé de l'Université et mathématicien de métier dans sa vie professionnelle !
Le sophisme.
Récidivant, le contradicteur imprudent est allé jusqu'à m'accuser de sophiste ! Là encore, il emploie un terme dont il ne connaît pas la signification.
Les sophistes, par exemple Zénon d'Elée, sont à l'origine des sophismes qui sont des raisonnements d'apparence logique mais conduisant à des conclusions fausses considérées néanmoins à tort comme vraies. Voir par exemple le sophisme d'Achille et de la tortue de Zénon d'Elée (cité dans le poème de Paul Valéry : Le cimetière marin).
Et là encore, l'ignorant péremptoire affirme des croyances personnelles étrangères au sujet et là encore il prétend donner des leçons en logique à un mathématicien qui maîtrise aussi la logique mathématique, discipline dont il ne connaît pas un traître mot ! Demandez- lui donc de démontrer le théorème d'incomplétude de l'arithmétique de Kurt Gödel !
Alors, que faire dans ce cas ? Eh bien, si on préfère les échanges sérieux et sereins, on abandonne à son sort ce genre de personnage qui ne se complaît que dans les conflits.
Il y a quand même mieux de quoi s'occuper !
Certes va-t-il réagir à sa façon, la mauvaise ! Peu importe, j'ai dit ce que j'avais à dire et je m'en tiendrai là car ce n'est pas moi qui ai raison, c'est la mathématique dont je ne suis que l'humble intermédiaire.
Formes indéterminées.
Bien entendu, d'après ce personnage, c'est moi, mathématicien de métier qui ne connaît rien aux mathématiques !
Récemment, j'ai évoqué ce que l'on appelle en mathématiques des formes indéterminées. Ce sont des expressions mathématiques pour lesquelles il est impossible d'affecter une valeur précise. Par exemple, l'expression indéterminée 0/0 n'a aucun sens. Il en est de même de n/0 quelque que soit le nombre n.
On rencontre aussi des formes indéterminées avec l'infini noté ∞.
Par exemple, les formes 1/∞, ∞/∞, ∞ multiplié par ∞, ∞/0, ∞ -∞ etc. sont des formes indéterminées ce qui signifie, retenez le bien ! qu'il est impossible de leur donner un résultat précis.
Or, cet intervenant qui, manifestement n'a que des connaissances rudimentaires en mathématiques a prétendu avec conviction, que ∞ - ∞ = ∞ ! Or, cette expression est fausse car on a vu qu'il est impossible de donner un résultat à une forme indéterminée, or ∞ - ∞ est une forme indéterminée d'où la contradiction de cet entêté ignorant qu'il ignore les mathématiques !
Eh bien, il a poussé l'inconscience jusqu'à vouloir donner une leçon de mathématiques à un mathématicien dument diplômé de l'Université et mathématicien de métier dans sa vie professionnelle !
Le sophisme.
Récidivant, le contradicteur imprudent est allé jusqu'à m'accuser de sophiste ! Là encore, il emploie un terme dont il ne connaît pas la signification.
Les sophistes, par exemple Zénon d'Elée, sont à l'origine des sophismes qui sont des raisonnements d'apparence logique mais conduisant à des conclusions fausses considérées néanmoins à tort comme vraies. Voir par exemple le sophisme d'Achille et de la tortue de Zénon d'Elée (cité dans le poème de Paul Valéry : Le cimetière marin).
Et là encore, l'ignorant péremptoire affirme des croyances personnelles étrangères au sujet et là encore il prétend donner des leçons en logique à un mathématicien qui maîtrise aussi la logique mathématique, discipline dont il ne connaît pas un traître mot ! Demandez- lui donc de démontrer le théorème d'incomplétude de l'arithmétique de Kurt Gödel !
Alors, que faire dans ce cas ? Eh bien, si on préfère les échanges sérieux et sereins, on abandonne à son sort ce genre de personnage qui ne se complaît que dans les conflits.
Il y a quand même mieux de quoi s'occuper !
Certes va-t-il réagir à sa façon, la mauvaise ! Peu importe, j'ai dit ce que j'avais à dire et je m'en tiendrai là car ce n'est pas moi qui ai raison, c'est la mathématique dont je ne suis que l'humble intermédiaire.

Esculape- Chef

- Messages : 1885
Date d'inscription : 31/07/2021
Age : 97
Localisation : Ile de France
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
@Esculape ....
Sophisme de la double faute:
Exemple:
« Esculape, ne tire pas les cheveux de ton frère ! C'est mal !
— Et alors maman, Darbut m'a pincé ! »
Sophisme de la double faute:
Exemple:
« Esculape, ne tire pas les cheveux de ton frère ! C'est mal !
— Et alors maman, Darbut m'a pincé ! »

Edouard de Montmonrency- Vénérable

- Messages : 20687
Date d'inscription : 02/01/2022

Esculape- Chef

- Messages : 1885
Date d'inscription : 31/07/2021
Age : 97
Localisation : Ile de France
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
... Ni vos images, ni vos formules, ne contredisent votre sophisme de la double faute. (votre concurrence victimaire) ... ça illustre juste votre vacuité sur ce sujet.

Edouard de Montmonrency- Vénérable

- Messages : 20687
Date d'inscription : 02/01/2022
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
"Si un âne te donne un coup de pied, ne lui rends pas." (Socrate)

Esculape- Chef

- Messages : 1885
Date d'inscription : 31/07/2021
Age : 97
Localisation : Ile de France
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Par contre gare au coup de sabot !Esculape a écrit:"Si un âne te donne un coup de pied, ne lui rends pas." (Socrate)


Jeannot Lapin- Sage

- Messages : 9233
Date d'inscription : 31/07/2021
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Oui.Jeannot Lapin a écrit:Par contre gare au coup de sabot !Esculape a écrit:"Si un âne te donne un coup de pied, ne lui rends pas." (Socrate)
Moralité : Se tenir à l'écart des ânes.

Esculape- Chef

- Messages : 1885
Date d'inscription : 31/07/2021
Age : 97
Localisation : Ile de France
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
... Un conseil, évite les miroirs ;-)Esculape a écrit:
Moralité : Se tenir à l'écart des ânes.

Edouard de Montmonrency- Vénérable

- Messages : 20687
Date d'inscription : 02/01/2022
 Remarque générale.
Remarque générale.
Je crois qu'il n'y a rien de plus primaire (pour ne pas dire "primate"), que l'expression "C'est pas moi, c'est toi" !
Il se dégage de cette "cinglante" réplique un amusant et touchant infantilisme !
Il se dégage de cette "cinglante" réplique un amusant et touchant infantilisme !

Esculape- Chef

- Messages : 1885
Date d'inscription : 31/07/2021
Age : 97
Localisation : Ile de France
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
... Oui monsieur ad hominem. (ça montre et démontre votre niveau)Esculape a écrit:Je crois qu'il n'y a rien de plus primaire (pour ne pas dire "primate"), que ... blablabla ...

Edouard de Montmonrency- Vénérable

- Messages : 20687
Date d'inscription : 02/01/2022
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
les ânes savent les chemins à ne pas emprunter, et que des têtes de mules cherchent en vain sans y parvenir de les dresser à leurs façons , avec le risque que les têtes de mules se font botter leurs derrières par les ânes !Esculape a écrit:Oui.Jeannot Lapin a écrit:Par contre gare au coup de sabot !Esculape a écrit:"Si un âne te donne un coup de pied, ne lui rends pas." (Socrate)
Moralité : Se tenir à l'écart des ânes.

Frère Barnabé- Vénérable

- Messages : 29046
Date d'inscription : 11/05/2017
Age : 61
Localisation : saint Etienne
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Pourquoi as t-on besoin d'un symbole infini pour effectuer des calculs?
Les limites ] +1/∞[ etc enfin vous voyez de quoi je parle, quels sont leurs objectifs?
L'infini c'est peut-être uniquement pour dire que l'on ne peut pas calculer une limite mmm de temps, d'espace
D'ailleurs quand on dérive, à quoi cela peut-il servir?
Ma réponse c'est:
De calculer le coefficient directeur et donc l’équation d’une tangente.
De déterminer, avant de faire un graphique, les intervalles où la fonction est croissante ou décroissante.
Mais j'ai utilisé les dérivés pour d'autres calculs comme la recherche d'équilibre dans une équation mais j'ai déjà oublié.
Les limites ] +1/∞[ etc enfin vous voyez de quoi je parle, quels sont leurs objectifs?
L'infini c'est peut-être uniquement pour dire que l'on ne peut pas calculer une limite mmm de temps, d'espace

D'ailleurs quand on dérive, à quoi cela peut-il servir?
Ma réponse c'est:
De calculer le coefficient directeur et donc l’équation d’une tangente.
De déterminer, avant de faire un graphique, les intervalles où la fonction est croissante ou décroissante.
Mais j'ai utilisé les dérivés pour d'autres calculs comme la recherche d'équilibre dans une équation mais j'ai déjà oublié.


Oligark- Impétrant

- Messages : 526
Date d'inscription : 31/01/2022
Edouard de Montmonrency aime ce message
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Oligark a écrit:Pourquoi as t-on besoin d'un symbole infini pour effectuer des calculs?
Les limites ] +1/∞[ etc enfin vous voyez de quoi je parle, quels sont leurs objectifs?
L'infini c'est peut-être uniquement pour dire que l'on ne peut pas calculer une limite mmm de temps, d'espace
D'ailleurs quand on dérive, à quoi cela peut-il servir?
Ma réponse c'est:
De calculer le coefficient directeur et donc l’équation d’une tangente.
De déterminer, avant de faire un graphique, les intervalles où la fonction est croissante ou décroissante.
Mais j'ai utilisé les dérivés pour d'autres calculs comme la recherche d'équilibre dans une équation mais j'ai déjà oublié.
Peut-être, ça veut peut-être dire qu'on est confiné dans un espace et un temps ad vitam aeternam.

Edouard de Montmonrency- Vénérable

- Messages : 20687
Date d'inscription : 02/01/2022
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
L'infini n'étant pas un nombre ne saurait intervenir dans des calculs mais, le cas échéant, indique si le calcul d'une expression dépendante de x par exemple, tend vers l'infini ou vers une limite avec x tendant vers l'infini ou vers zéro.Oligark a écrit:Pourquoi as t-on besoin d'un symbole infini pour effectuer des calculs?
Les limites ] +1/∞[ etc enfin vous voyez de quoi je parle, quels sont leurs objectifs?
L'infini c'est peut-être uniquement pour dire que l'on ne peut pas calculer une limite mmm de temps, d'espace
D'ailleurs quand on dérive, à quoi cela peut-il servir?
Ma réponse c'est:
De calculer le coefficient directeur et donc l’équation d’une tangente.
De déterminer, avant de faire un graphique, les intervalles où la fonction est croissante ou décroissante.
Mais j'ai utilisé les dérivés pour d'autres calculs comme la recherche d'équilibre dans une équation mais j'ai déjà oublié.
Exemple : L'expression sin(x)/x tend vers 1 lorsque x tend vers zéro alors que la relation 0/0 n'a pas de sens, relation que l'on obtient si on fait x = 0 dans sin(x)/x car sin(0) = 0.
Votre exemple concernant les dérivées relève de l'enseignement secondaire et pour accéder à la mathématique de la physique de pointe, le niveau requis est au moins de bac +6
Je suis à votre disposition pour, amicalement, préciser certains points qui pourraient vous intéresser car je soupçonne chez vous un désir d'apprendre qui vous honore.


Esculape- Chef

- Messages : 1885
Date d'inscription : 31/07/2021
Age : 97
Localisation : Ile de France
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Il y a bien longtemps que je ne m'intéresse plus à l'astrophysique, me réservant en physique, à la mécanique quantique et à la cosmologie s ans oublier la Relativité générale. Ma mémoire n'et plus ce qu'elle fut et mes neurones commencent à renâcler ...
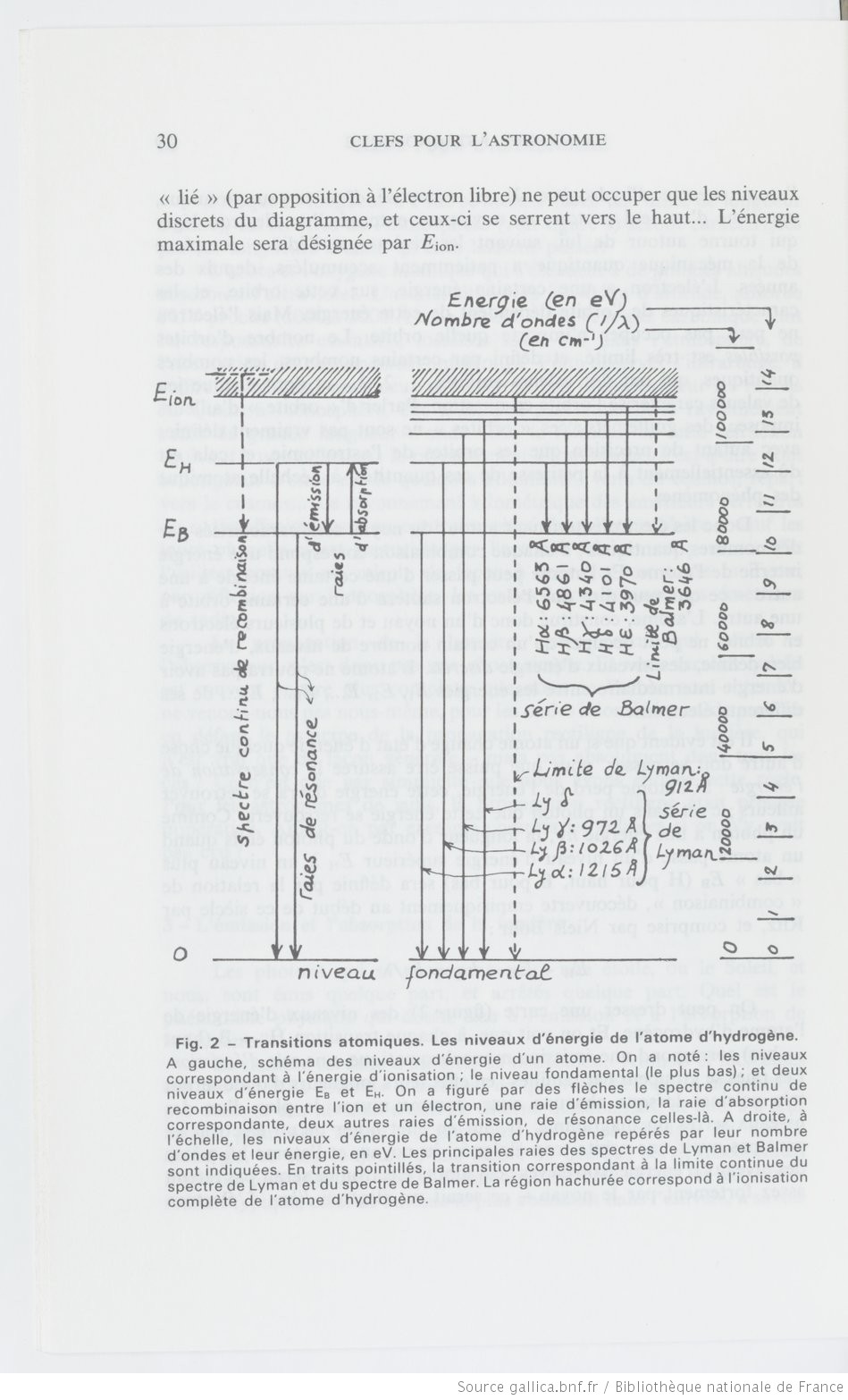
Je me souviens seulement des formules de Lyman* : 1/λ = Rb(1-1/n²) (Rb constante de Rydberg) et de λ=Bµ/(µ²-n²) pour Balmer**.
Et encore, je ne suis même pas certain que ces formules soient les bonne ! Mes souvenirs en ce domaine remontent à l'âge où j'avais 30 ans lorsque j'étais l'assistant de Jean Claude Pecker.
Mais je me souviens que ces formules ont été découvertes empiriquement et justifiées plus tard en mécanique quantique.
Vous vous êtes arrêté à bac + 5 ! Chouette, si c'est en sciences exactes, voilà qui promet des échanges fructueux et intéressants !
P.S. Il me semble reconnaître un document de Pecker, mais c'est trop vague pour que j'en sois certain.
* Limite de Lyman pour n tendant vers l'infini.
** Aux environs de λ = 360nm pour imite de Balmer.

Esculape- Chef

- Messages : 1885
Date d'inscription : 31/07/2021
Age : 97
Localisation : Ile de France
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Oui c'est bien un document de J.C. Pecker. Non pas en sciences exactes une branche des sciences appliquées. Raison pour laquelle certains sujets m'intéressent moins, la théorie des nombres par exemple je n'y comprends rien du tout et d'ailleurs je ne comprends pas pourquoi on s'y intéresse. Un nombre entier ou non cela reste un nombre et je ne comprends pas pourquoi on accorde de l'importance à une division d'un nombre ou non par lui même.
Merci pour votre réponse, je comprends un peu mieux les transitions atomiques.
Merci pour votre réponse, je comprends un peu mieux les transitions atomiques.

Oligark- Impétrant

- Messages : 526
Date d'inscription : 31/01/2022
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Ne classeriez vous pas l'astrophysique parmi les sciences exactes ? Voilà qui me surprend beaucoup !Oligark a écrit:Oui c'est bien un document de J.C. Pecker. Non pas en sciences exactes une branche des sciences appliquées. Raison pour laquelle certains sujets m'intéressent moins, la théorie des nombres par exemple je n'y comprends rien du tout et d'ailleurs je ne comprends pas pourquoi on s'y intéresse. Un nombre entier ou non cela reste un nombre et je ne comprends pas pourquoi on accorde de l'importance à une division d'un nombre ou non par lui même.
Merci pour votre réponse, je comprends un peu mieux les transitions atomiques.
Je crois que n'être pas intéressé paru ne branche du savoir n'est pas une preuve de l'inutilité de cette branche.
Quant à la théorie des nombres premiers, elle est liée à la physique via la fonction ζ(s) de Riemann.
Toute la mathématique est intriquée avec la physique, c’est ça que les profanes comprennent le moins et pourtant c’est vrai.
Je préfère préciser, on ne sait jamais ! que je ne mets aucun sens péjoratif au mot "profane", car nus sommes tous profanes en quelque chose !
Je ne me souviens pas avoi traité les "transitions atomiques" (?). Rafraichissez moi les idées, j'ai oublié. Merci.
Mais il m'est arrivé de parler de la nucléosynthèse, ce qui est différent.

Esculape- Chef

- Messages : 1885
Date d'inscription : 31/07/2021
Age : 97
Localisation : Ile de France
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Oui la fonction zéta je sais mais je ne comprends pas ce que recherche Riemann. Si l'astrophysique en fait partie, je trouve juste étrange d'utiliser le mot exacte.
Je parlais de l'énergie d'ionisation avec les différents niveaux c'est tout c'est une partie du livre de M. Pecker.
Je parlais de l'énergie d'ionisation avec les différents niveaux c'est tout c'est une partie du livre de M. Pecker.

Oligark- Impétrant

- Messages : 526
Date d'inscription : 31/01/2022
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
La spectroscopie est une science exacte,Oligark a écrit:Oui la fonction zéta je sais mais je ne comprends pas ce que recherche Riemann. Si l'astrophysique en fait partie, je trouve juste étrange d'utiliser le mot exacte.
Je parlais de l'énergie d'ionisation avec les différents niveaux c'est tout c'est une partie du livre de M. Pecker.
La loi de déplacement de Wien est exacte,
L'effet Doppler est exact,
L'effet Zeeman est exact,
La distance des étoiles calculée grâce aux Céphéides donne des résultats exacts,
La distance des astres plus lointains, par les supenovae de type 1a donne des résultats exacts.
La distance d'astres encore plus lointains s'obtient avec une excellente approximation à l'aide de la loi de Hubble.
L'évolution des étoiles à partir de leur type spectral est exacte,
La théorie des étoiles à neutrons est exacte,
Etc.
L'astrophysique, qui n'utilisent que des lois ou des théories exactes est un science exacte.

Esculape- Chef

- Messages : 1885
Date d'inscription : 31/07/2021
Age : 97
Localisation : Ile de France
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
... En Sciences et en maths (qui sont pourtant des sciences dures), tout est exact ... jusqu'à preuve du contraire (qui relativise l'ancienne exactitude).
Bref, c'est l'exactitude qui progresse, pas à pas. ;-)
Bref, c'est l'exactitude qui progresse, pas à pas. ;-)

Edouard de Montmonrency- Vénérable

- Messages : 20687
Date d'inscription : 02/01/2022
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Très bien, cela permet de se rassurer que cela soit exact. J'ai une question farfelue : le titre est
"Bref aperçu sur l'infini"
1 : Nous ne pouvons pas avoir un aperçu de l'infini puisqu'il est infini
2 : l'infini au sens de l'univers n'existe pas, c'est une notion abstraite,
l'univers physique contient tout ce qui est physique et rien d'autre. Cet énoncé semble trivial, mais il est plus profond qu'il n'y paraît. Il dit en particulier que l'univers n'est pas un objet physique comme les autres. Tout objet a un bord, même si celui-ci n'est pas net, comme dans le cas du Soleil ou d'une galaxie.
3 : futura sciences : l'infini lui est indispensable pour appréhender le fini. Un exemple immédiat est le calcul du nombre π, rapport entre la circonférence d'un cercle et son diamètre. Il s'agit d'une longueur finie, mais son expression est un nombre comportant une infinité de décimales. Pour calculer ce nombre (Archimède l'avait déjà tenté), il faut utiliser un processus infini.
Il semble difficile de donner une définition à l'infini, vous y convenez?
"Bref aperçu sur l'infini"
1 : Nous ne pouvons pas avoir un aperçu de l'infini puisqu'il est infini
2 : l'infini au sens de l'univers n'existe pas, c'est une notion abstraite,
l'univers physique contient tout ce qui est physique et rien d'autre. Cet énoncé semble trivial, mais il est plus profond qu'il n'y paraît. Il dit en particulier que l'univers n'est pas un objet physique comme les autres. Tout objet a un bord, même si celui-ci n'est pas net, comme dans le cas du Soleil ou d'une galaxie.
3 : futura sciences : l'infini lui est indispensable pour appréhender le fini. Un exemple immédiat est le calcul du nombre π, rapport entre la circonférence d'un cercle et son diamètre. Il s'agit d'une longueur finie, mais son expression est un nombre comportant une infinité de décimales. Pour calculer ce nombre (Archimède l'avait déjà tenté), il faut utiliser un processus infini.
Il semble difficile de donner une définition à l'infini, vous y convenez?

Oligark- Impétrant

- Messages : 526
Date d'inscription : 31/01/2022
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Oligark a écrit:Très bien, cela permet de se rassurer que cela soit exact. J'ai une question farfelue : le titre est
"Bref aperçu sur l'infini"
1 : Nous ne pouvons pas avoir un aperçu de l'infini puisqu'il est infini
2 : l'infini au sens de l'univers n'existe pas, c'est une notion abstraite,
l'univers physique contient tout ce qui est physique et rien d'autre. Cet énoncé semble trivial, mais il est plus profond qu'il n'y paraît. Il dit en particulier que l'univers n'est pas un objet physique comme les autres. Tout objet a un bord, même si celui-ci n'est pas net, comme dans le cas du Soleil ou d'une galaxie.
3 : futura sciences : l'infini lui est indispensable pour appréhender le fini. Un exemple immédiat est le calcul du nombre π, rapport entre la circonférence d'un cercle et son diamètre. Il s'agit d'une longueur finie, mais son expression est un nombre comportant une infinité de décimales. Pour calculer ce nombre (Archimède l'avait déjà tenté), il faut utiliser un processus infini.
Il semble difficile de donner une définition à l'infini, vous y convenez?
Oui, ce que l'on appelle l'infini (théorique et mathématique) est fini en pratique pour nous (délimité dans notre espace et temps de notre Univers.) ... au delà de notre "infini" il y a probablement d'autres infinis (faits de multivers ou de je ne sais de quoi). C'est ma conception personnelle.

Edouard de Montmonrency- Vénérable

- Messages : 20687
Date d'inscription : 02/01/2022
 POUR OLIGGARK
POUR OLIGGARK
Pour Oligark seulement.
Pour raisonner avec compétence sur l'infini dans l'Univers, il faut d'abord être au courant de la cosmologie moderne qui n'a plus grand chose à voir avec la théorie vulgarisée du Big bang.
La théorie de "l'énergie sombre" qui montre que cette énergie se comporte comme une gravitation répulsive a complètement changé la donne pour des raisons bien trop mathématiquement compliquées pour être exposées ici.
De plus, la théorie de "l'inflation éternelle" achève de donner le coup de grâce à la cosmologie d'hier.
Conclusion : Ne plus réfléchir aujourd'hui à partir de la Théorie du Big bang d'hier toujours correcte dans ses grandes lignes mais considérablement enrichie. Et c'est cet enrichissement primordial qu'il est impératif de connaître.
Amicalement.
Pour raisonner avec compétence sur l'infini dans l'Univers, il faut d'abord être au courant de la cosmologie moderne qui n'a plus grand chose à voir avec la théorie vulgarisée du Big bang.
La théorie de "l'énergie sombre" qui montre que cette énergie se comporte comme une gravitation répulsive a complètement changé la donne pour des raisons bien trop mathématiquement compliquées pour être exposées ici.
De plus, la théorie de "l'inflation éternelle" achève de donner le coup de grâce à la cosmologie d'hier.
Conclusion : Ne plus réfléchir aujourd'hui à partir de la Théorie du Big bang d'hier toujours correcte dans ses grandes lignes mais considérablement enrichie. Et c'est cet enrichissement primordial qu'il est impératif de connaître.
Amicalement.

Esculape- Chef

- Messages : 1885
Date d'inscription : 31/07/2021
Age : 97
Localisation : Ile de France
 Re: Bref aperçu sur l'infini.
Re: Bref aperçu sur l'infini.
Esculape a écrit:Pour Oligark seulement....
L'ostracisation est ta méthode ?
(si c'est le cas, c'est d'une infinie bêtise)

Edouard de Montmonrency- Vénérable

- Messages : 20687
Date d'inscription : 02/01/2022
Page 4 sur 6 •  1, 2, 3, 4, 5, 6
1, 2, 3, 4, 5, 6 
Page 4 sur 6
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum